第二次专家在线研讨题答疑辑要
发布者:李样明 发布时间:2015-11-16 浏览数:5774
根据《数学辞海》, 角是指以具有公共端点的两条射线为界的平面部分。 一般地, 人们在脑海中将角就是对应于如下图形d:
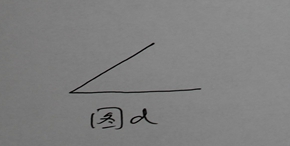
但是这就不确切, 因为图形d有下图e 与图f 之分。
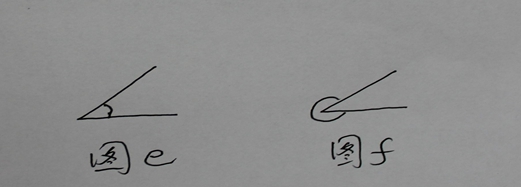
为区分不同的角, 我们就规定了角的大小(度量):1度的角为 周角的360分之一。 当然, 按照上面的规定,角的度数只能是在0 与360 之间。但是这不能满现实生活的要求, 如: 高台跳水运动员的转体的幅度与方向如何刻画?
因此角又有另外的定义:一条射线绕固定端点从一个位置旋转到另一个位置而扫过的平面部分。(《数学辞海》)
这样角就有所谓的静态的与动态的两种定义。 按照动态的定义, 我们就有了超过360度的角了,并且根据旋转的方向,也可以定义正角、负角及零角等概念,就形成任意角的概念。 所谓任意角, 就是任意大小的角。 “大小” 在实数范围, 就有正、负、零之分, 这也是 正角、负角及零角的来历。
在小学阶段, 由于认知能力有限, 教材的编写是以生活中的例子来引入角的概念的, 故在人们提起角的概念, 一般还是联想到图e的角; 到了初中阶段, 人们主要还是用静态的定义来理解角的概念, 讨论图d的角时, 还是联想到图e的角, 但是也注意到了 图f的角, 如 讨论三角形的外角的等概念时。 到了高中阶段, 就要强调用动态的定义来理解角, 显示了我们对角的定义的更高的观点。 原因一是解决实际问题的需要, 二是为接下来学习角的三角函数做准备。 作为高中教师应该理解角的概念的形成, 这样我们在教学中就能居高临下。
回到我们研讨题二。 在初中阶段, 人们习惯上将角的认识停留在图e的角, 即锐角, 故问题(1)中要区分三种情况来讨论。 到了高中阶段, 我们的认识更高了一个层次, 就应该想到用更高的观点来看此问题, 即 图a, b, c 三种情形统一性问题。 统一了之后的结果还覆盖了问题(3) 的情形。这样在考虑正角的情况下,下图a, b, c 三种情形中的∠B, ∠D, ∠E的关系可以统一表示为
∠B + ∠D = ∠E。
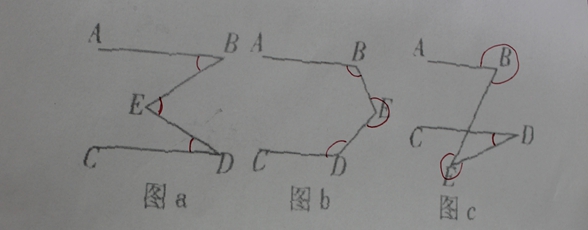
另外, 在图c中, 如果 规定∠B,∠E取正值,∠D取负值, 则它们之间也有关系:
∠B + ∠D = ∠E。

我们十分欣慰的是, 学员们参与讨论比较广泛, 也都表达了类似的观点,并且能学以致用,联系于教学来讨论, 这说明学员们有比较高的认知水平。

- 薛志坚
- 到访时间:2015-11-29

- 钟建华
- 到访时间:2015-11-27

- 熊彦
- 到访时间:2015-11-23

- 吴捷云
- 到访时间:2015-11-18

- 数学孟胜奇
- 到访时间:2015-11-23

- 数学陈静安
- 到访时间:2015-11-28

- 陈燕芬
- 到访时间:2015-11-22

- 李样明
- 到访时间:2015-11-28